Genetic parameters and genetic progress of economically important traits in a long-term selected Duroc pig population
-
摘要:目的
对受长期选择的实际杜洛克猪育种群体3个重要经济性状进行遗传参数估计,分析各性状取得的遗传进展,并探讨实际育种群体中长期选择等因素对群体遗传参数的影响。
方法收集广西某种猪场核心育种群杜洛克猪2003—2018年共计15 760条生长性能测定记录。运用DMU软件的DMUAI模块和DMU4模块,利用多性状动物模型估计3个重要经济性状的群体遗传参数和个体育种值。并通过估计该群体的年度累计群体遗传参数以评估该群体在长期选择过程中遗传参数的变化情况。
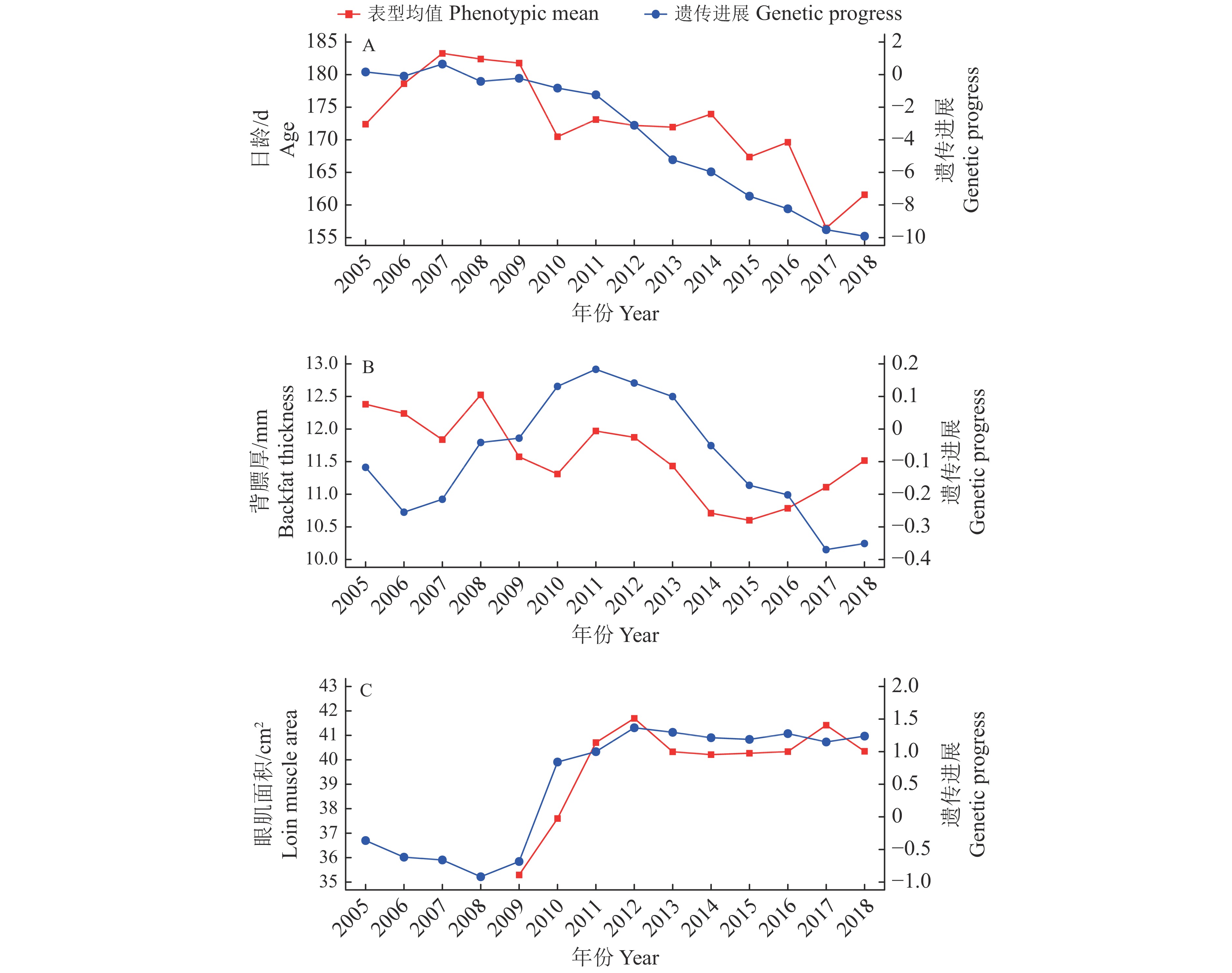
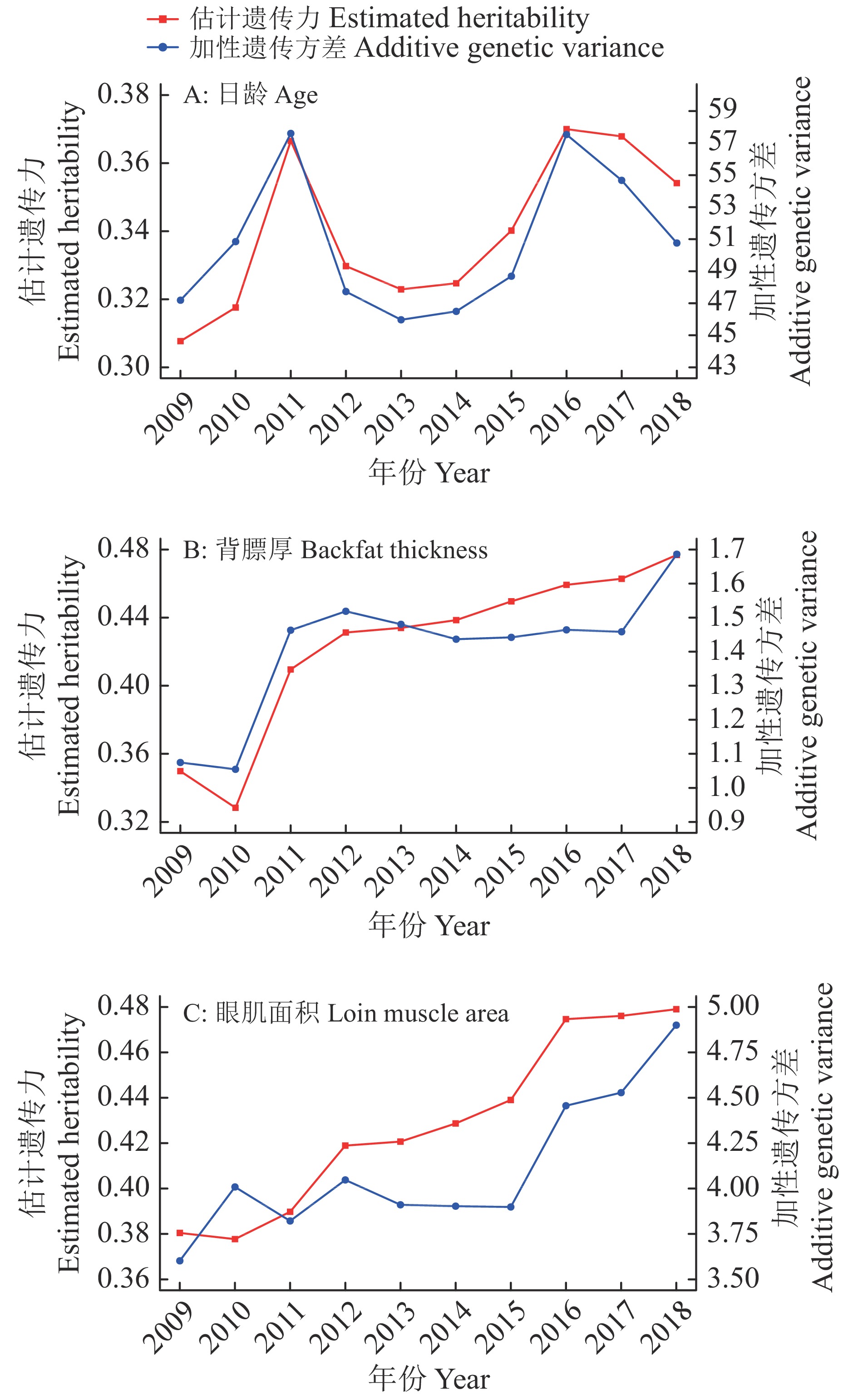
结果杜洛克猪3个重要经济性状(达100 kg体质量日龄、背膘厚和眼肌面积)的估计遗传力分别为0.354、0.477和0.479,均属中高遗传力性状。3个性状间的遗传相关范围为−0.110~0.039,表型相关范围为−0.076~0.082,均属于弱相关。性状达100 kg体质量日龄在长期选择中取得了较大的遗传进展,而性状达100 kg体质量背膘厚和达100 kg体质量眼肌面积取得的遗传进展较小。分析年度累积群体估计的遗传参数发现,3个经济性状的加性遗传方差出现了不同程度的变化。
结论杜洛克猪群体3个重要经济性状均为中高遗传力性状且性状间相关性较弱。在实际育种群体中,长期选择及引种等因素会导致群体遗传参数发生变化,育种实践中应及时开展遗传参数估计,以获得准确的遗传评估结果,加速群体遗传改良。
Abstract:ObjectiveTo estimate the genetic parameters of three economic traits in a long-term selection population, analyze their genetic progress, and investigate the factors including long-term selection affecting the genetic parameters in the practical breeding population.
MethodA total of 15 760 growth performance records of Duroc pigs were collected in a core breeding field from 2003 to 2018. Using DMUAI module and DMU4 module of DMU software, a multi-trait animal model was used to estimate the genetic parameters and breeding values of three important economic traits. We estimated the genetic parameters of annual accumulative population to evaluate the change of genetic parameters during the long-term selection.
ResultThe estimates of heritability for three important economic traits including age, backfat thickness and loin muscle area at 100 kg body weight were 0.354, 0.477 and 0.479, respectively. All three traits had medium-high heritability. There were low correlations among three economic traits. The genetic and phenotypic correlations ranged from −0.110 to 0.039 and from −0.076 to 0.082, respectively. Among three traits, age at 100 kg body weight had relatively greater genetic progress in long-term selection, while backfat thickness at 100 kg body weight and loin muscle area at 100 kg body weight had relatively less genetic progress. Furthermore, the additive genetic variance changed in different degrees for three economic traits by estimating the genetic parameters of the annual accumulative population.
ConclusionThese traits of this Duroc pig population had the medium-high estimates of heritability and low correlations. Moreover, long-term selection and introduction could lead to the changing of genetic parameters. Therefore, genetic parameters should be estimated timely to obtain accurate genetic evaluation for accelerating the genetic improvement in breeding practice.
-
Keywords:
- Duroc pig /
- long-term selection /
- multi-trait animal model /
- genetic parameter /
- genetic progress
-
土壤可见−近红外反射光谱是土壤理化特性光谱行为的综合,土壤中许多组分在可见−近红外光谱范围内具有反射与吸收特征,可以用来识别土壤成分[1]。土壤反射光谱法是一种无破坏性、快速、经济的方法,已广泛应用于土壤矿物、物理、化学和生物学特性的预测[2-3]。土壤游离铁是成土母质风化、迁移转化的产物,能够反映成土过程和成土环境,是表征土壤发育程度的指标之一[4]。在中国土壤系统分类中,土壤游离铁含量是判断低活性富铁层、铁质特性和水耕人为土中铁聚、铁渗特征的指标[5]。
近年来,国内外学者在利用土壤反射光谱预测铁氧化含量和矿物类型方面开展了研究。Coleman等[6]认为红光波段(630~690 nm)和近红外波段(1 150~1 300 nm)是解释美国阿拉巴马州变性土和淋溶土铁氧化物变异的最重要波段。彭杰等[7]对湖南土壤研究表明,氧化铁含量对土壤光谱反射率有明显的影响,利用土壤线性参数预测氧化铁含量具有可行性。夏学齐等[8]研究江苏土壤发现铁氧化物含量和类型均可以在土壤反射率光谱或其一阶导数值中找到相关波段,反射光谱方法能够定量铁氧化物总量、鉴别针铁矿和赤铁矿及相对含量。Summers等[9]报道预测澳大利亚南部土壤铁氧化物的波段是400~1 100 nm,不同类型和矿物组成的土壤氧化铁偏最小二乘回归(Partial least squares regression,PLSR)预测模型需要进行校准。谢碧裕[10]研究江西丘陵地区水稻土时认为PLSR模型为土壤氧化铁含量最优估测模型。熊俊峰等[11]利用PLSR对全反射波段与江苏东台市土壤中不同形态铁含量进行建模预测,结果表明多元散射矫正光谱处理建立的模型最优。郭颖等[12]研究表明珠江三角洲地区水稻土无定型铁的敏感波段为404、574、784、854和1 204 nm等,BP人工神经网络(Back propagation neural network,BPNN)模型预测土壤无定型铁含量的效果最佳。Xu等[13]报道浙江土壤游离铁的特征波段是400~480、1 900和2 200 nm,PLSR模型预测土壤游离铁准确性高。Camargo等[14]报道预测巴西氧化土游离铁和赤铁矿最准确的光谱波段为380~800 nm,预测模型为PLSR模型。Sellitto等[15]认为土壤针铁矿和赤铁矿含量分别与420和535 nm波段二阶导数处理的谱带振幅呈显著相关性,反射光谱可用来快速测定巴西氧化土中氧化铁矿物。Rossel等[16]报道可见−近红外反射光谱可以用于估算澳大利亚表层土壤中赤铁矿和针铁矿的相对丰度,特征波段分别是880和920 nm。Bahia等[17-18]报道利用PLSR模型预测巴西土壤游离铁准确度高,原始反射光谱经过二阶微分和去包络线处理后对赤铁矿和针铁矿预测效果好。而魏昌龙等[19]研究表明PLSR和BPNN模型均不能准确预测安徽宣城土壤游离铁含量。以上研究为利用可见−近红外反射光谱预测土壤铁氧化物含量提供了依据,但对于不同区域和类型的土壤,精确预测铁氧化物的光谱转换、敏感或特征波段和预测模型均不一致,因此有必要建立不同区域土壤铁氧化物的光谱预测模型。广西位于我国华南地区,风化和淋溶作用强,脱硅富铁铝化明显,铁铝等元素以二三氧化物形态残留富集,使得该地区土壤中氧化铁矿物主导了土壤的颜色,从而明显区别于其他区域。利用土壤光谱特征定量反演广西土壤游离铁含量的研究鲜见报道,本文通过分析广西旱地土壤反射光谱与游离铁含量的关系,试图建立基于可见−近红外光谱的土壤游离铁含量预测模型,为该区域土壤游离铁含量预测提供一种简单、快速、经济的方法。
1. 材料与方法
1.1 土壤采集与分析
2015年12月至2017年12月采集广西壮族自治区82个旱地土壤剖面的B层土壤(图1),土壤类型包括雏形土、淋溶土、富铁土和铁铝土等。土壤样品经室内风干后,制备过60和100目筛的样品,结合参考文献[20]的方法进行土壤化学特性分析。土壤游离铁含量的测定用连二亚硫酸钠−柠檬酸钠−碳酸氢钠(DCB)浸提−邻菲罗啉比色法;土壤全铁含量测定用HNO3-HCl-HClO4消解−邻啡罗啉比色法;土壤有机质含量测定用重铬酸钾−浓硫酸−外加热法。土壤化学性质分析于2016年3月至2018年2月完成。选取过60目筛的土壤于2017年12月至2018年8月进行光谱的采集与处理。
1.2 土壤光谱数据的获取与光谱变换处理
土壤光谱用AvaField-3便携式地物波谱仪(荷兰Avantes公司)测定,其波长范围是350~2 500 nm,采样间隔为0.6(区间为300~1 000 nm)和6 nm(区间为1 000~2 500 nm),光谱分辨率为1.4(300~1 100 nm)和15 nm(1 100~2 500 nm),波长重复性为 ± 0.3 nm,输出波段为1 569 nm。光谱测定在可控制光照条件的暗室内进行,光源为一盏50 W的卤素灯,光源通过光纤连接探头,视场角为10°。土壤样品放置于直径2.5 cm、高1.5 cm黑色瓶盖中,将土样表面刮平。探头距土样表面2~3 mm垂直进行光谱数据采集,测试之前先进行白板校正,每个土样采集25条光谱曲线,算术平均后得到该土样的实际反射光谱数据。每个土样的光谱曲线去除噪声较大的边缘波段(350~399和2 401~2 500 nm),保留400~2 400 nm波段的反射光谱数据用于后续研究。
在土壤原始光谱反射率基础上进行数学形式变换可以有效减少光照、背景噪声的干扰,提高光谱灵敏度,更加容易分解混合特征信息[21]。为筛选对土壤游离铁含量敏感的特征波段,本研究对土壤原始光谱进行10种变换处理,分别是一阶微分、二阶微分、倒数、倒数的对数、倒数的一阶微分、倒数的二阶微分、去包络线、平方根、平方根的一阶微分和平方根的二阶微分。用Pearson相关系数(rλ)来衡量光谱变换后光谱反射率与土壤游离铁含量间相关程度,其计算公式如下:
$${r_{_\lambda} } = \frac{{\displaystyle\sum\limits_{i = 1}^n {\left( {{x_i} - \overline x } \right)} \left( {{y_i} - \overline y } \right)}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{\left( {{x_i} - \overline x } \right)}^2}\displaystyle\sum\limits_{n = 1}^n {{{\left( {{y_i} - \overline y } \right)}^2}} } } }},$$ (1) 式中,xi为第i个波段反射率,yi为第i个土壤游离铁含量,
$ \overline x $ 为波段反射率的平均值,$\overline y $ 为土壤游离铁含量的平均值。1.3 建模样本和验证样本的划分
将供试土壤按游离铁含量高低排序后随机选取建模和验证样本。建模和验证样本数分别为62和20,占总样本的75%和25%。通过SPSS 21.0对2组数据进行K-S检验[12],得到D=0.58、P=0.74>0.05,故可确认这两组样本来自同一分布。各样本集土壤游离铁含量的箱型散点图见图2,供试土壤基本理化性质统计如下:全铁(Fe2O3)为9.37~124.44 g/kg,均值为(57.58±27.26) g/kg,变异系数为47.35%,游离铁(Fe2O3)为1.58~108.13 g/kg,均值为(41.88±24.03) g/kg,变异系数为57.35%,有机质为2.20~48.90 g/kg,均值为(12.13±8.86) g/kg,变异系数为73.04%。
1.4 模型建立与验证
偏最小二乘回归(PLSR)可以很好地解决各变量内部高度线性相关、样本个数少于变量个数等问题,很大程度上提高了模型的应用能力、精度及可靠性[22]。逐步多元线性回归(SMLR)则将变量逐个选入回归方程,并考虑全部变量的方差贡献值,期间利用F统计量选择或剔除自变量,不断重复,直到无法引入新变量,最终建立自变量与因变量之间的回归关系[23]。本研究采用PLSR和SMLR方法建立土壤游离铁含量预测模型,分别在MATLAB 2016a和SPSS 21.0软件中实现。
模型的预测精度通过预测值与实测值的决定系数(R2)、均方根误差(RMSE)以及相对预测偏差(RPD)来评价;R2及RPD越大、RMSE越小,说明预测效果越好[24]。当R2>0.90,RPD>3.00时,模型具有极好的预测能力;当0.82<R2<0.90,2.50<RPD<3.00时,模型具有很好的预测能力;当0.66<R2<0.81,2.00<RPD<2.50时,模型具有近似定量预测能力;当0.50<R2<0.66,1.50<RPD<2.00时,模型具有对样品高含量与低含量进行区分的可能性;当R2< 0.50时,RPD≤1.50时,模型不能成功预测[25]。R2、RMSE和RPD计算公式如下:
$$R^{2} {\rm{ = }}\frac{{\displaystyle\sum\limits_{i = 1}^n {\left( {{{\mathop y\limits^ \wedge }_i} - \overline y } \right)} }}{{\displaystyle\sum\limits_{i = 1}^n {\left( {{y_i} - \overline y } \right)} }},$$ (2) $${\rm{RMSE}} = \sqrt {\sum\limits_{i = 1}^n {\frac{{{{\left( {{y_i} - {{\hat y}_i}} \right)}^{2}}}}{n}} } ,$$ (3) $${\rm{RPD}} = \frac{{{\rm{SD}}}}{{{\rm{RMSE}}}},$$ (4) 式中,
${y_i}$ 为第i个样本的土壤游离铁实测值;$\mathop {{y_i}}\limits^ \wedge $ 为第i个样本的土壤游离铁预测值;$\overline y $ 为82个样本土壤游离铁实测平均值;SD为土壤游离铁实测值的标准差;n为样本数。2. 结果与分析
2.1 土壤游离铁含量的光谱特征
供试土壤游离铁含量分为<20、20~40、40~60及>60 g·kg−1 4组,对应的样本数分别为13、33、18和18,对每一组别样本计算原始光谱反射率和去包络线处理平均值,形成不同土壤游离铁含量的光谱曲线(图3)。由图3a可知,在400~2 400 nm土壤游离铁含量与光谱反射率呈负相关关系,即随着土壤游离铁含量的增加,土壤光谱反射率降低;在可见光波段(400~780 nm)范围内光谱曲线呈明显的上升趋势,氧化铁含量越高,光谱反射率越低,在400 nm波段附近有一个小吸收谷;在近红外波段(780~1 300 nm)范围内光谱反射率上升比较平缓,在1 300~1 600 nm波段光谱曲线趋于重合,说明光谱曲线的差异较小;在1 400、1 900及2 200 nm附近存在明显的曲线吸收特征,主要是与铁的氧化物及高岭类黏土矿物所含OH−有关[26]。由图3b可知,在400 nm附近的吸收谷与氧化铁含量有关,氧化铁含量高的比较清晰;不同游离铁含量的土壤在800 nm附近有明显的吸收峰,900 nm附近有吸收谷。
2.2 光谱变换形式与土壤游离铁含量的相关性
将土壤游离铁含量与原始光谱、去包络线、一阶微分、二阶微分、倒数、倒数一阶微分、倒数二阶微分、倒数的对数、平方根、平方根一阶微分和平方根二阶微分变换后的光谱反射率进行Pearson相关性分析,由分析结果(图4)可知,原始光谱反射率与游离铁含量呈负相关,并且整条曲线比较平滑,很难筛选出与游离铁含量具有良好相关性的敏感波段,而经过光谱变换后的土壤光谱反射率与游离铁含量之间的相关性明显提高。为筛选预测土壤游离铁的不同光谱变换形式下的特征波段,对每种光谱变换后土壤光谱反射率与游离铁含量的相关系数进行P=0.01水平的显著性检验(|r0.01|=0.29)。去包络线光谱变换主要是突出了一些反射峰和吸收谷的信息,在可见光波段范围内相关系数绝对值最大达到0.60,其他波段相关系数绝对值最大值约为0.20。倒数、倒数的对数与平方根光谱变换光谱曲线基本是原始光谱曲线以x轴为对称轴的相似图,整体表现比较平缓。微分变换处理效果显著,多处波段相关系数绝对值≥0.50,一阶微分变换比二阶微分变换整体效果要好。从全波段来看,效果最好的光谱变换形式是倒数一阶微分。基于以上分析结果,选取通过显著性检验波段数量多的一阶微分、去包络线、倒数、倒数一阶微分和平方根一阶微分的光谱变换形式建立土壤游离铁预测模型,评估不同光谱变换后土壤游离铁含量预测精度。
2.3 不同反射光谱建模波段的确定
不同学者利用不同光谱波段建立同一土壤属性预测模型的结果不尽相同[10, 12]。然而,很少有学者对基于不同反射光谱波段建立的预测模型效果进行评估,针对某种土壤属性选择较优的建模波段。
根据供试土壤在可见−近红外波段的光谱反射率与土壤游离铁含量的相关关系,获取与土壤游离铁含量相关性较强的反射光谱建模波段。本研究中在全波段400~2 400 nm范围内随着土壤游离铁含量增加,土壤光谱反射率降低,因此选择400~2 400 nm波段作为全波段数据。通过不同光谱变换后的光谱反射率与土壤游离铁含量相关性分析得知,经过一阶微分、去包络线、倒数、倒数一阶微分和平方根一阶微分的光谱变换,在400~580和760~1 300 nm波段范围内有明显的反射和吸收特征,因此确定为土壤游离铁的特征波段。将光谱反射率与土壤游离铁含量的相关系数经过P=0.01水平的显著性检验,再通过逐步多元线性的方法剔除共线性波段,得到400、457、510、735、848 nm等12个敏感波段。敏感波段光谱反射率与土壤游离铁含量间的相关系数以及方差膨胀因子见表1。
表 1 敏感波段共线性检验1)Table 1. Collinearity test of sensitive band光谱变换
Pectral transformationλ(敏感)/nm
Sensitive band皮尔逊相关系数
Pearson correlation coefficient容差
Tolerance方差膨胀因子
Variance inflation factor一阶微分
First order differential735 0.43** 1.00 1.00 847 −0.49** 1.00 1.00 去包络线
Continuum removal456 0.55** 0.17 5.96 1 102 −0.43** 0.99 1.01 倒数 Reciprocal 400 0.64** 0.19 5.18 510 0.41** 0.19 5.18 倒数一阶微分
Reciprocal first order differential498 −0.78** 0.54 1.84 2 191 0.63** 0.54 1.84 平方根一阶微分
Square root first order differential457 −0.64** 0.59 1.69 848 −0.48** 0.65 1.54 1 028 0.49** 0.92 1.08 1 759 −0.50** 0.90 1.11 1)**表示0.01水平显著相关
1) ** represents 0.01 level of significant correlation2.4 土壤游离铁含量的预测模型
利用全波段、特征波段和敏感波段建立土壤游离铁含量预测模型(表2)。结果表明,基于全波段进行倒数和倒数的一阶微分光谱变换的SMLR模型,验证样本的R2分别为0.80和0.82,RPD分别为2.20和2.21,模型具有近似定量预测能力;PLSR模型的验证样本R2<0.80,RPD<2.0,模型不能进行定量预测。基于特征波段一阶微分光谱变换的SMLR模型,验证样本的R2为0.85,RPD为2.62,模型具有很好的预测能力;PLSR模型的验证样本R2 <0.80,RPD<2.0,模型不能进行定量预测。基于敏感波段建模效果不理想,SMLR和PLSR模型验证集 R2<0.80,除倒数一阶微分外,RPD<2.0,模型不能进行定量预测。
表 2 土壤游离铁含量预测模型1)Table 2. Calibration and validation of the model for predicting soil free iron content光谱变换
Spectral transformationSMLR PLSR 建模样本
Calibration set验证样本
Validation set建模样本
Calibration set验证样本
Validation setR2 RMSE/
(g·kg−1)R2 RMSE/
(g·kg−1)RPD 主成分
个数R2 RMSE/
(g·kg−1)R2 RMSE/
(g·kg−1)RPD 全波段 Full band FD 0.85 8.92 0.28 19.53 1.13 10 0.99 2.25 0.64 14.27 1.54 CR 0.76 12.16 0.62 17.86 1.23 3 0.51 16.10 0.69 15.56 1.42 RT 0.87 8.28 0.80 10.34 2.20 4 0.61 14.52 0.78 12.26 1.68 RTFD 0.89 7.61 0.82 9.97 2.21 9 0.96 2.85 0.69 13.80 1.60 SRFD 0.89 7.65 0.45 19.77 1.11 12 1.00 0.91 0.67 13.22 1.67 特征波段 Characteristic band FD 0.89 7.68 0.85 8.41 2.62 7 0.96 4.42 0.64 13.15 1.68 CR 0.83 9.77 0.78 10.00 2.20 3 0.84 9.44 0.68 11.81 1.87 RT 0.63 14.11 0.75 10.97 2.01 8 0.90 9.77 0.77 11.14 1.98 RTFD 0.89 7.73 0.40 17.08 1.29 3 0.71 12.61 0.71 13.13 1.68 SRFD 0.89 7.77 0.80 10.74 2.05 5 0.91 7.11 0.71 13.26 1.66 敏感波段 Sensitive band FD 0.56 15.34 0.59 14.22 1.55 2 0.64 13.89 0.64 14.09 1.56 CR 0.74 11.90 0.71 13.75 1.60 4 0.74 11.67 0.69 11.75 1.88 RT 0.70 12.70 0.48 15.36 1.43 4 0.63 13.96 0.61 13.13 1.68 RTFD 0.81 10.04 0.60 13.62 1.62 3 0.83 10.10 0.79 10.31 2.20 SRFD 0.65 13.71 0.65 12.52 1.76 2 0.68 13.13 0.67 12.75 1.73 1) FD为一阶微分;CR为去包络线;RT为倒数;RTFD为倒数一阶微分;SRFD为平方根一阶微分;R2为决定系数;RMSE为均方根误差;RPD为相对分析误差;全波段是400~2 400 nm;特征波段是400~580和760~1 300 nm;敏感波段是400、457、510、735、848 nm等12个波段
1) FD is first order differential; CR is continuum removal; RT is reciprocal; RTFD is reciprocal first order differential; SRFD is square root first order differential; R2 is determination coefficient; RMSE is root mean squared error; RPD is relative percent deviation; Full bands are 400−2 400 nm; Characteristic bands are 400−580 and 760−1 300 nm; Sensitive bands are twelve bands including 400, 457, 510, 735, 848 nm, et al图5为通过3种反射光谱建模波段建立的土壤游离铁含量最佳反演模型的实测值与预测值散点图。综合比较R2、RMSE和RPD评价指标可知,基于特征波段一阶微分光谱变换的SMLR模型预测土壤游离铁含量的效果最佳。土壤游离铁含量的最佳预测模型表示为:
![]() 图 5 不同建模波段最佳模型的土壤游离铁含量a:全波段倒数一阶微分逐步多元线性回归模型; b:特征波段一阶微分逐步多元线性回归模型; c:敏感波段倒数一阶微分偏最小二乘回归模型Figure 5. Soil free iron content of the optimal model in different modeling banda: Reciprocal first differential method using the SMLR model in the full bands; b: First differential method using the SMLR model in the feature bands; c: Reciprocal first differential method using the PLSR model in the sensitive bands
图 5 不同建模波段最佳模型的土壤游离铁含量a:全波段倒数一阶微分逐步多元线性回归模型; b:特征波段一阶微分逐步多元线性回归模型; c:敏感波段倒数一阶微分偏最小二乘回归模型Figure 5. Soil free iron content of the optimal model in different modeling banda: Reciprocal first differential method using the SMLR model in the full bands; b: First differential method using the SMLR model in the feature bands; c: Reciprocal first differential method using the PLSR model in the sensitive bands$$\begin{split} Y = & - 21\;670.551 {X_{457\;{\rm{nm}}}} + 20\;332.458 {X_{1\;154\;{\rm{nm}}}} - \\ & 68\;210.736 {X_{892\;{\rm{nm}}}} - 18\;131.561 {X_{1\;251\;{\rm{nm}}}}- \\ & 7\;618.486 {X_{1\;078\;{\rm{nm}}}} - 17\;822.473 {X_{969\;{\rm{nm}}}} + \\ & 44\;266.188 {X_{940\;{\rm{nm}}}} - 27\;588.766 {X_{890\;{\rm{nm}}}} + \\ & 29\;868.990 {X_{781\;{\rm{nm}}}} - 11\;733.883 {X_{1\;087\;{\rm{nm}}}} + \\ & 14.309 \text{,} \end{split} $$ 式中,Y表示土壤游离铁含量预测值;X表示提取的该波段处的土壤光谱反射率。
3. 结论与讨论
广西旱地土壤随着游离铁含量的增加,可见−近红外波段范围内土壤光谱反射率降低,在可见光波段的降低程度比近红外波段高,可见光波段能够提供更多的游离铁信息。土壤原始光谱经过微分光谱变换后光谱反射率与土壤游离铁含量的相关性显著提高。采用一阶微分光谱变换、特征波段(400~580、760~1 300 nm)和逐步多元线性回归建立的模型能够很好地预测广西旱地土壤游离铁含量,验证样本的R2和RPD分别为0.85和2.62。
本研究的相关性分析结果表明,土壤游离铁含量在全波段范围内与原始光谱呈负相关关系,且特征波段位于可见近红外光(400~1 300 nm)区域,在457和900 nm波段附近具有明显的氧化铁吸收谷特征,在800 nm波段附近有氧化铁反射峰特征。该结论同前人的研究结论一致[27],同时也符合土壤特征光谱的产生机制[7, 13]。其中,400~580、760~1 300、400、457、510 nm等波段是本研究区域土壤游离铁的特征波段和敏感波段,其主要原因是不同土壤铁氧化物含量有差异,且不同的氧化物中羟基的数量也会对其敏感波段造成影响[14-16]。其次,光谱变换形式及波段提取方法的不同,使得同一土壤属性提取的特征波段不一致。本文提取特征波段是在相关分析的前提下,相关系数通过P=0.01显著性检验;敏感波段是进一步采用多元逐步线性手段剔除共线性波段获取的。本研究中土壤游离铁含量的反射光谱在可见光波段,反射率曲线从长波向短波波段明显下降,可见光波段反射率的降低程度高于近红外波段,这主要是由土壤铁氧化物的电子跃迁造成的,也就是说在可见光范围内能够提供更多的氧化铁信息[7]。进入红外波段后,不同游离氧化铁含量梯度的光谱曲线在1 400、1 900、2 200 nm附近有强烈的吸收谷,这几个吸收谷是受到N—H、C—H、C—O、C=O等功能基团的影响[3]。这与赵小敏等[1]、郭颖等[12]、黄应丰等[26]对我国南方其他区域土壤光谱特征的研究结果一致。
本研究中原始光谱反射率与土壤游离铁含量的相关性整体偏低,经过一阶微分、二阶微分、倒数、倒数的对数等10种形式变换后,微分光谱变换的光谱反射率与游离铁含量之间相关性显著提高,其中倒数一阶微分变换的相关系数提高最多,相关系数绝对值最大为0.64。熊俊峰等[11]利用全波段数据对不同铁元素含量进行反演时认为多元散射校正(MSC)光谱处理效果最好。何挺等[27]计算不同变换形式反射率与氧化铁含量的相关系数表明,变换后相关性并没有得到显著增强,只有反射率平方根的一阶微分相关系数提高最多;Xu等[13]将氧化铁进行对数光谱变换后得到较好的预测模型。光谱变换能够降低外界噪声干扰,突出光谱特征,增强光谱反射率与土壤属性的相关性,提高基于土壤光谱预测土壤属性的精确性,然而不同光谱变换方法的建模精度存在差异[11-13]。根据不同光谱波段建模结果可知,利用特征波段(400~580、760~1 300 nm)的建模效果要优于全波段(400~2 400 nm)。研究表明不同区域和不同类型土壤,基于可见−近红外反射光谱预测土壤铁氧化物的光谱变换、特征波段及预测模型均不一致。与其他区域土壤[7, 9, 10, 12-13]不同的是,广西旱地B层土壤中有机质含量较少,均值仅为12.13 g/kg,而土壤游离铁和全铁含量较高。全波段由于波段较多相应地增加了受其他因素或成分影响的程度,使得不仅没有凸显全面而丰富的氧化铁光谱特征信息,反而使得一些重要波段信息被掩盖[7]。
一元线性回归、偏最小二乘回归、逐步多元线性回归、反向神经网络(BPNN)等是利用光谱特征预测土壤属性最普遍的建模方法。本研究选用PLSR和SMLR这2种模型来预测土壤游离铁含量,通过R2、RMSE和RPD评价,SMLR建模效果要优于PLSR,与何挺等[27]用逐步回归分析得到氧化铁的预测模型结论一致;但众多研究结果[10, 11, 13-14, 17]表明PLSR模型能较好地预测土壤铁氧化物含量。造成这种结果的原因可能是:1)研究区土壤类型多样,不同的土壤类型的反射光谱不同[24],而光谱反射率建立在反演模型的基础上,因此对反演结果造成影响;2)由于土壤成分复杂,当土壤氧化铁含量不高时,其他成分易对其光谱特征造成交叉干扰[13]。不同研究区域土壤中水分含量、有机质以及盐分等差异较大,模型结果自然也有较大不同。本文虽然已经尽可能排除了这些影响,但成土母质及众多含量较少成分的影响仍难以排除,还需要继续深入研究。本研究中SMLR预测模型应用于验证样本的R2和RPD分别为0.85和2.62,与浙江[13]、巴西[14,18]土壤游离铁预测模型相近,高于江苏省东台[11]、安徽宣城[19]土壤游离铁预测模型,结果表明本研究中建立的广西旱地土壤游离铁预测模型准确度较高。从不同游离铁含量的光谱特征曲线图[24]可以看出,本研究区供试土壤光谱曲线类型属于铁影响型光谱曲线,相对来说这类光谱曲线土壤中有机质含量低,铁氧化物含量高于有机质控制型光谱曲线。根据谢碧裕[10]、郭颖等[12]研究不同区域水稻土的氧化铁含量预测模型可知,对来自不同地区不同发育母质的同一类型土壤进行预测时,其预测精度同样不能保证。因此,本研究预测模型综合考虑了土壤光谱反射率的影响因素,选择室内光谱测试环境,以避免外界环境的影响;统一土壤化学分析测定与光谱预测时的土壤粒径,并且选用自然风干的B层土壤,最大程度降低了土壤其他组分对氧化铁光谱反演结果的影响。已有研究表明土壤有机质影响土壤铁含量与光谱反射率关系,尤其是在可见光区域[28],有机质含量对游离铁估算精度的影响小于全铁、无定型铁[11]。为了降低有机质对游离铁含量预测精度可能的影响,本研究只选取有机质含量低的B层土壤,有关土壤有机质含量对广西旱地土壤游离铁预测精度产生怎样的影响以及本研究得到的游离铁预测模型是否适用于更广泛的土壤亟待进一步深入研究。
-
表 1 杜洛克猪群体达100 kg体质量时3个经济性状表型的描述性统计
Table 1 The descriptive statistics of the phenotype for three economic traits of Duroc pig population at 100 kg body weight
指标
Index日龄/d
Age背膘厚/mm
Backfat thickness眼肌面积/cm2
Loin muscle area平均值 Mean 170.38 11.49 40.29 标准差 Standard deviation 15.50 1.94 3.54 最小值 Minimum 115.91 4.65 23.22 中位数 Median 168.70 11.33 40.53 最大值 Maximum 248.16 23.43 56.42 记录数 No. of records 15 754 15 757 13 233 表 2 杜洛克猪群体达100 kg体质量时3个经济性状的方差分析F值1)
Table 2 F value in the variance analysis for three economic traits of Duroc pig population at 100 kg body weight
因素
Factor日龄
Age背膘厚
Backfat thickness眼肌面积
Loin muscle area场 Farm 4929.15** 203.41** 815.35** 年份 Year 117.74** 79.63** 228.13** 季节 Season 31.46** 96.55** 33.56** 性别 Sex 849.87** 357.13** 453.14** 1)“**”表示影响达到0.01的显著水平
1)“**”indicates the effect at 0.01 significance level表 3 杜洛克猪群体达100 kg体质量时3个经济性状估计方差组分及估计遗传力1)
Table 3 The variance components and estimated heritability for three economic traits of Duroc pig population at 100 kg body weight
指标
Index日龄
Age背膘厚
Backfat thickness眼肌面积
Loin muscle area$ {{\sigma }}_{\rm{a}}^{\rm{2}} $ 50.761 1.686 4.900 $ {{\sigma }}_{\rm{e}}^{\rm{2}} $ 92.584 1.850 5.329 $ {{\sigma }}_{\rm{p}}^{\rm{2}} $ 143.345 3.536 10.229 $ {{h}}^{\rm{2}} $±SE 0.354±0.018 0.477±0.018 0.479±0.021 1) $ {\rm{\sigma }}_{\rm{a}}^{\rm{2}} $:加性遗传方差, $ {\rm{\sigma }}_{\rm{e}}^{\rm{2}} $:残差方差, $ {\rm{\sigma }}_{\rm{p}}^{\rm{2}} $:表型方差, $ {{h}}^{\rm{2}} $:遗传力,SE:标准误
1) $ {\rm{\sigma }}_{\rm{a}}^{\rm{2}} $: Additive genetic variance, $ {\rm{\sigma }}_{\rm{e}}^{\rm{2}} $: Residual variance, $ {\rm{\sigma }}_{\rm{p}}^{\rm{2}} $: Phenotypic variance, $ {{h}}^{\rm{2}} $: Heritability, SE:Standard error表 4 杜洛克猪群体达100 kg体质量时3个经济性状的遗传相关与表型相关1)
Table 4 The genetic correlations and phenotypic correlations for three economic traits of Duroc pig population at 100 kg body weight
性状
Trait日龄
Age背膘厚
Backfat thickness眼肌面积
Loin muscle area日龄
Age−0.076 0.032 背膘厚
Backfat thickness−0.110(0.038) 0.082 眼肌面积
Loin muscle area0.031(0.043) 0.039(0.038) 1) 右上角数字为性状间的表型相关,左下角数字为性状间的遗传相关(括号中为遗传相关标准误)
1) Numbers at above diagonal are phenotypic correlations between traits, and the ones at below diagonal are genetic correlations between traits (the standard error of genetic correlation in bracket)表 5 杜洛克猪达100 kg体质量时3个经济性状的年度累积群体遗传参数1)
Table 5 The genetic parameters of annual cumulative population for three economic traits of Duroc pigs at 100 kg body weight
年份
Year日龄
Age背膘厚
Backfat thickness眼肌面积
Loin muscle area$ {{\sigma }}_{\rm{a}}^{\rm{2}} $ $ {{\sigma }}_{\rm{e}}^{\rm{2}} $ $ {{h}}^{\rm{2}} $±SE $ {{\sigma }}_{\rm{a}}^{\rm{2}} $ $ {{\sigma }}_{\rm{e}}^{\rm{2}} $ $ {{h}}^{\rm{2}} $±SE $ {{\sigma }}_{\rm{a}}^{\rm{2}} $ $ {{\sigma }}_{\rm{e}}^{\rm{2}} $ $ {{h}}^{\rm{2}} $±SE 2009 47.191 106.179 0.308±0.039 1.075 1.997 0.350±0.039 3.602 5.866 0.380±0.107 2010 50.847 109.264 0.318±0.036 1.055 2.158 0.328±0.034 4.009 6.604 0.378±0.067 2011 57.602 99.554 0.367±0.029 1.463 2.109 0.410±0.028 3.822 5.983 0.390±0.039 2012 47.727 97.014 0.330±0.025 1.519 2.003 0.431±0.024 4.047 5.614 0.419±0.031 2013 45.969 96.388 0.323±0.023 1.480 1.931 0.434±0.023 3.911 5.385 0.421±0.027 2014 46.494 96.699 0.325±0.022 1.437 1.839 0.439±0.022 3.903 5.202 0.429±0.026 2015 48.689 94.439 0.340±0.021 1.442 1.766 0.450±0.021 3.899 4.982 0.439±0.025 2016 57.533 97.974 0.370±0.020 1.464 1.724 0.459±0.020 4.456 4.933 0.475±0.023 2017 54.674 93.961 0.368±0.019 1.458 1.693 0.463±0.019 4.528 4.984 0.476±0.022 2018 50.761 92.584 0.354±0.018 1.686 1.850 0.477±0.018 4.900 5.329 0.479±0.021 1) $ {\rm{\sigma }}_{\rm{a}}^{\rm{2}} $:加性遗传方差, $ {\rm{\sigma }}_{\rm{e}}^{\rm{2}} $:残差方差, $ {{h}}^{\rm{2}} $:遗传力,SE:标准误
1) $ {\rm{\sigma }}_{\rm{a}}^{\rm{2}} $: Additive genetic variance, $ {\rm{\sigma }}_{\rm{e}}^{\rm{2}} $: Residual variance, $ {{h}}^{\rm{2}} $: Heritability, SE:Standard error -
[1] 李学武, 王瑞军, 王志英, 等. 家畜遗传评估方法研究进展[J]. 中国农业大学学报, 2020, 25(2): 54-60. [2] 乔国艳, 袁超, 郭婷婷, 等. 不同数据结构和动物模型对高山美利奴羊经济性状遗传参数估计的比较[J]. 中国畜牧兽医, 2020, 47(2): 531-543. [3] DONG L, TAN C, CAI G, et al. Estimates of variance components and heritability using different animal models for growth, backfat, litter size, and healthy birth ratio in Large White pigs[J]. Canadian Journal of Animal Science, 2020, 100(2): 330-336. doi: 10.1139/cjas-2019-0136
[4] 张胜利, 杨秀文, 靳明武, 等. 遗传参数不同估计方法的比较[J]. 遗传, 1995, 17(6): 21-23. doi: 10.3321/j.issn:0253-9772.1995.06.006 [5] ALENCARIANO J D S F, ELIAS N M, CLAUDIO N C, et al. Effects of the number of animals in the numerator relationship matrix on variance components for milk yield using restricted maximum likelihood and Bayesian methods[J]. Revista Brasileira de Zootecnia, 2009, 38(8): 1468-1477. doi: 10.1590/S1516-35982009000800011
[6] BEERLI P. Comparison of Bayesian and maximum-likelihood inference of population genetic parameters[J]. Bioinformatics, 2006, 22(3): 341-345. doi: 10.1093/bioinformatics/bti803
[7] 高虹, 邱小田, 王长存, 等. 我国杜洛克、长白、大白猪区域性联合遗传评估研究[J]. 畜牧兽医学报, 2018, 49(12): 2567-2575. doi: 10.11843/j.issn.0366-6964.2018.12.005 [8] SU H, GOLDEN B, HYDE L, et al. Genetic parameters for carcass and ultrasound traits in Hereford and admixed Simmental beef cattle: Accuracy of evaluating carcass traits[J]. Journal of Animal Science, 2017, 95(11): 4718-4727. doi: 10.2527/jas2017.1865
[9] 姚天雄, 陈冬, 吴珍芳, 等. 大白和长白猪大样本群体的繁殖性状遗传参数估计及影响因素分析[J]. 畜牧兽医学报, 2019, 50(11): 2195-2207. doi: 10.11843/j.issn.0366-6964.2019.11.003 [10] HOLM B, BAKKEN M, KLEMETSDAL G, et al. Genetic correlations between reproduction and production traits in swine[J]. Journal of Animal Science, 2004, 82(12): 3458-3464. doi: 10.2527/2004.82123458x
[11] WOLF J, ZAKOVA E, GROENEVELD E. Genetic parameters for a joint genetic evaluation of production and reproduction traits in pigs[J]. Czech Journal of Animal Science, 2005, 50(3): 96-103.
[12] LOPEZ B I M, SONG C, SEO K. Genetic parameters and trends for production traits and their relationship with litter traits in Landrace and Yorkshire pigs[J]. Animal Science Journal, 2018, 89(10): 1381-1388. doi: 10.1111/asj.13090
[13] HOQUE M A, KADOWAKI H, SHIBATA T, et al. Maternal and direct genetic parameters for production traits and maternal correlations among production and feed efficiency traits in Duroc pigs[J]. Asian-Australasian Journal of Animal Sciences, 2008, 21(7): 961-966. doi: 10.5713/ajas.2008.70641
[14] 张勤. 我国猪育种现状与挑战[J]. 北方牧业, 2019(10): 12-13. [15] SHARMA D, JOHARI D C, KATARIA M C, et al. Factors affecting direct and correlated responses in a White Leghorn population under long term selection for egg number[J]. British Poultry Science, 1998, 39(1): 31-38. doi: 10.1080/00071669889358
[16] R CORE TEAM. R: A language and environment for statistical computing[DB/CD]. R Foundation for Statistical Computing, 2019.
[17] MADSEN P, JENSEN J, LABOURIAU R, et al. DMU:A package for analyzing multivariate mixed models in quantitative genetics and genomics[C]//ASAS. 10th World Congress on Genetics Applied to Livestock Production, Vancouver:American Society of Animal Science, 2014.
[18] 曹洪战, 吴常信, 师守堃. 利用MTDFREML估计大约克双肌臀种猪活体背膘厚遗传力时固定效应及水平数的确定[J]. 中国畜牧杂志, 2004, 40(3): 34-36. doi: 10.3969/j.issn.0258-7033.2004.03.014 [19] DARFOUR-ODURO K A, NAAZIE A, AHUNU B K, et al. Genetic parameter estimates of growth traits of indigenous pigs in Northern Ghana[J]. Livestock Science, 2009, 125(2): 187-191.
[20] JIAO S, MALTECCA C, GRAY K A, et al. Feed intake, average daily gain, feed efficiency, and real-time ultrasound traits in Duroc pigs: I: Genetic parameter estimation and accuracy of genomic prediction[J]. Journal of Animal Science, 2014, 92(6): 2377-2386. doi: 10.2527/jas.2013-7338
[21] LOPEZ B I M, SEO K S, SONG C W, et al. Estimation of genetic parameters and accuracy of genomic prediction for production traits in Duroc pigs[J]. Czech Journal of Animal Science, 2019, 64(4): 160-165. doi: 10.17221/150/2018-CJAS
[22] 庄站伟, 付帝生, 丁荣荣, 等. 美系杜洛克种猪体尺性状遗传参数估计及其与生长性状的关系研究[J]. 广东农业科学, 2018, 45(7): 121-125. [23] 曹建新, 齐莹莹, 王钰龙, 等. 基于多性状动物模型估计大白猪、长白猪生长性状的遗传参数[J]. 畜牧与兽医, 2017, 49(11): 154-156. [24] ZHANG Z, ZHANG H, PAN R, et al. Genetic parameters and trends for production and reproduction traits of a Landrace herd in China[J]. Journal of Integrative Agriculture, 2016, 15(5): 1069-1075. doi: 10.1016/S2095-3119(15)61105-4
[25] 刘榜, 蒋腾飞, 樊斌, 等. 外种猪遗传改良进展与发展趋势[J]. 猪业科学, 2011, 28(9): 106-108. doi: 10.3969/j.issn.1673-5358.2011.09.035 [26] 楼平儿, 华坚青. 应用BLUP法选择加系约克夏种猪的遗传进展分析[J]. 畜牧与兽医, 2002, 34(10): 16-17. doi: 10.3969/j.issn.0529-5130.2002.10.009 [27] CHATTERJEE R N, MISRA B S, SINGH H N. Time trends of genetic parameters in a White Leghorn population subjected to long term single trait selection[J]. Indian Journal of Animal Sciences, 2002, 72(6): 465-468.
[28] 丁向东, 王长存, 周子文, 等. 生猪遗传改良计划实施以来我国猪主要经济性状进展分析[J]. 中国畜牧杂志, 2021, 57(1): 224-230. -
期刊类型引用(9)
1. 胡昕,买买提·沙吾提,张峰,崔锦涛,艾尼玩·艾买尔,阿斯娅·曼力克. 基于蒲公英优化随机森林模型的沙漠土壤Fe_2O_3含量高光谱遥感反演. 中国沙漠. 2025(02): 191-204 .  百度学术
百度学术
2. 张霞,孙友鑫,尚坤,丁松滔,孙伟超. 基于有机质特征谱段的土壤Cd含量高光谱遥感反演. 农业机械学报. 2024(01): 186-195 .  百度学术
百度学术
3. 孙东年,韩张雄,杨树俊,王思远,张贺. DCB浸提-电感耦合等离子体光谱法测定土壤中游离态铁. 化学工程师. 2023(02): 21-24 .  百度学术
百度学术
4. 晁增福,邢小宁. 夜间灯光数据与统计数据的相关性研究——以川南经济区为例. 数学的实践与认识. 2023(04): 100-110 .  百度学术
百度学术
5. 金鑫,翟婷,汪蓬,宋颖,汤珊珊,郑添元,谢泽龙. 黄土和红壤坡面侵蚀差异及其与土壤性质的关系. 水土保持学报. 2023(04): 118-123 .  百度学术
百度学术
6. 沈月,蔡玮,陈思力,颜军,董久鸣,陆若辉. 超声波提取-电感耦合等离子发射光谱法测定土壤中游离铁. 中国土壤与肥料. 2023(09): 241-244 .  百度学术
百度学术
7. 赵海龙,甘淑,王俊杰,胡琳. 土壤氧化铁的特征波长选择和高光谱反演. 中国生态农业学报(中英文). 2022(08): 1336-1345 .  百度学术
百度学术
8. 赵海龙,甘淑,袁希平,胡琳,刘帅,王俊杰. 基于多尺度连续小波分解的土壤氧化铁反演. 光学学报. 2022(22): 209-216 .  百度学术
百度学术
9. 俞越明,万梦雪,胡文友,王霞,王昌昆,周怡,吴秋梅,黄标. 基于光谱技术的土壤多参数快速检测进展与展望. 环境监控与预警. 2020(03): 26-32 .  百度学术
百度学术
其他类型引用(8)




 下载:
下载: