Effects of nitrogen, phosphorus and potassium levels on the growth of Neyraudia reynaudiana of soil and water conservation plant
-
摘要:目的
探索不同氮磷钾水平对类芦Neyraudia reynaudiana生长状况的影响.
方法采用营养液砂培试验,对优良水土保持植物类芦在不同氮、磷和钾供应水平下的响应规律进行了研究.
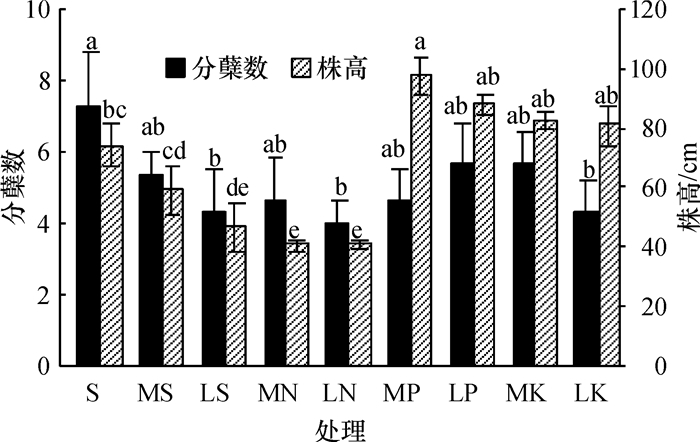
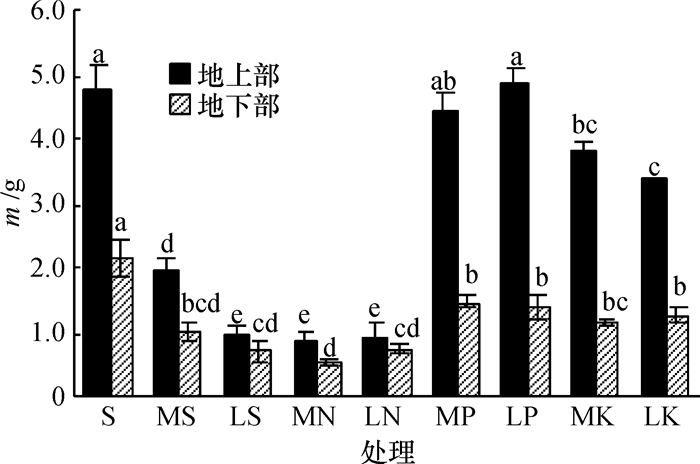
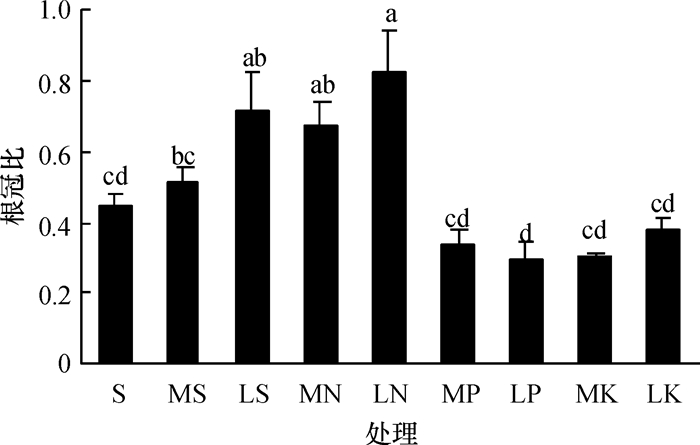
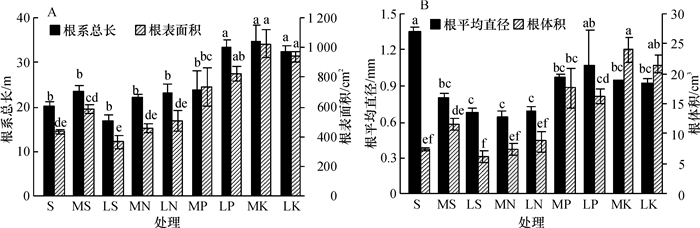
结果和结论0.750 mmol·L-1的氮和0.030 mmol·L-1的钾会显著影响类芦生长,降低类芦地上部和地下部生物量;低磷(0.005 mmol·L-1)对类芦地上部生物量无显著影响,但会显著降低地下部生物量;低磷和低钾(0.030 mmol·L-1)对类芦生长的影响显著小于0.750 mmol·L-1氮水平的影响,在低磷和低钾条件下,类芦根系长度和根表面积显著增加,表现出对低磷和低钾胁迫较强的适应和自我调节能力.用类芦进行植被恢复时,氮素的补充更为重要.
Abstract:ObjectiveTo explore the effects of nitrogen, phosphorus and potassium levels on the growth of burmareed, Neyraudia reynaudiana.
MethodNutrient solution-sand culture experiment was applied to study the response of burmareed which was a very excellent soil and water conservation plant at different nitrogen, phosphorus and potassium levels.
Result and conclusionThe results indicated that 0.750 mmol·L-1 N and 0.030 mmol·L-1 K significantly affected the burmareed growth and reduced the aboveground and underground biomass of burmareed. The concentration of 0.005 mmol·L-1 P did not affect the aboveground biomass, but significantly reduced the underground biomass. The effect of 0.750 mmol·L-1 N on the growth of burmareed was significantly stronger than that of 0.030 mmol·L-1 P and 0.030 mmol·L-1 K. In low P and K condition, burmareed could increase root length and surface area, which displayed its strong capacity of adapting and self-adjusting for low P and K stress. Supplement of nitrogen is very important for revegetation with burmareed.
-
Keywords:
- soil and water conservation plant /
- Neyraudia reynaudiana /
- nitrogen /
- biomass /
- root
-
随着农业转型和农村劳动力转移,农业生产从单一低价值的谷类农产品转向多样化高价值的农产品[1]。果茶园产业对经济发展具有至关重要的地位,我国的水果和茶叶种植面积与产量均位居世界前列。近年来,随着国家对农业机械化越来越重视,在资金上也加大了投入,山地果茶园运输机械有了较大发展,以华南农业大学、华中农业大学为代表的高校和相关单位相继研发出多种不同类型的山地果茶园运输装备,例如轮式[2]、履带式[3-4]、轨道式[5-7]等,然而农资农具的“快速随停随装卸”仍需要人工装卸,安全性和效率都很低。20世纪 90 年代至今,国内外自装卸运输车的设计研发已趋于成熟,但主要集中在集装箱运输、环卫等领域,专门针对农业的装卸运输车辆研究较少。王乐宁等[8]设计了一种方草捆捡拾堆垛机可完成草捆的装卸、运输、堆垛等。Babkov 等[9]设计了一种干草堆卡车,通过手指状的平台插入秸秆或干草在升降装置中完成装料,但不适用于丘陵山地多类型物资装卸。吴伟斌等[10]以山地果园轮式运输机为基础,研究设计了一种L型拉臂式自装卸装置。张成[11]设计加装了一种集升降、自卸功能于一体的作业平台,虽然满足了装卸需要但是运输效率较低。胡文武等[12]设计了一款加装旋转起重机电动双轨道运输车,但是旋转起重机装卸效率很低。现有的农用运输机往往只有自卸功能,运输装卸效率低,容易损伤农产品。物料和农资装卸缺乏合适的装卸装置和装卸方法,作业均由人工举升到平台上,到达目的地后再由人工搬运至地面,装卸过程耗费了大量的人力和时间[13]。本文基于华南农业大学与广东振声智能装备有限公司联合研制的电动单轨运输机,充分发挥“一机多用”的理念,提出了一种电动单轨运输机装卸设计方案,对摆臂式装卸结构进行了优化,以期进一步提升山地果茶园运输机械的功能和实用性。
1. 果茶园装卸方案设计与结构优化
1.1 摆臂式装卸方案设计
自走式电动单轨运输机适用于山地果茶园的肥料、农药、果品和生产工具等货物运输,解决了道路地形复杂、坡度陡峭的山地果园运输需求问题,其主要技术参数:电动机功率3.0 kW、配套电源48 V、行走速度0.9~1.0 m·s−1、最大装载质量300 kg、最大爬行坡度35°。根据单轨运输机的技术参数,本文提出一种山地果茶园单轨运输机装卸方案并设计了一种摆臂式装卸结构(图1),集成在运输平台上,设计的装卸装置最大装卸高度为 700 mm、装卸质量为 200 kg。
1.2 摆臂式装卸结构设计与分析
摆臂式装卸结构简图如图2, A 为油缸耳朵与底座左端的安装点, B 为举升臂旋转中心和举升臂下端铰孔与底座右端的安装点, C(C0、C1)为油缸推杆与举升臂铰孔的安装点,D(D0、D1)为举升臂上端铰孔,M为A点垂直方向和B点水平方向的支点;α0、α1 分别是举升臂的最小装卸角度和最大装卸角度,对应吊卸工况下的起始位置和极限工作位置,β 为推杆铰点相对旋转中心与举升臂的偏角; A 到 B 的水平、竖直距离分别为 L1、L2 ;B到D的距离(l1、l2 )为举升臂长度。设计举升臂长度 BD 为 600 mm;运输状态 D0 到 B 的相对高度( L3) 为 500 mm,以预留空间安放货箱锁具等部件。根据行业标准,单轨运输机轨道安装离地高度一般300~450 mm; B 离轨道高度约 200 mm,为满足极限高度情况下的装卸工作, B 离地高度最大为700 mm;卸货极限状态D1 到B 相对高度 (L4) 为 200 mm。
举升臂初始和极限位置与旋转角度的关系如下式:
$$ \mathrm{sin}{\alpha }_{0}=\dfrac{{L}_{3}}{l_1} \text{,} $$ (1) $$ \mathrm{sin}{\alpha }_{1}=-\dfrac{{L}_{4}}{l_{1}} 。 $$ (2) 为避免液压油缸的死点,装卸结构满足以下关系:
$$ \mathrm{\angle }ABM < \alpha -\beta < \angle ABM+180^\circ \text{,} $$ (3) $$ \mathrm{\angle }ABM=\mathrm{arctan}\dfrac{{L}_{2}}{{L}_{1}} 。 $$ (4) 由式(1)和(2)得 α0=56.44°、α1=199.47°,即举升机构装卸工作时最小和最大的装卸角度分别为 56.44°和199.47°。考虑到单轨运输机总体尺寸,并满足单轨运输机装卸过程中极限位置,设计L1 为 640 mm、L2 为 100 mm、B和 C之间的距离(d)为 140 mm、β 为 35°。举升臂的推拉依靠油缸传递的驱动力,油缸实际工作压力的大小与负载(举升臂的工作状态)有关,以 B 为坐标原点、水平向右为 x 轴,建立平面坐标系,并进行受力分析,对 B 点举升臂所受力矩平衡,可得:
$$ \left\{\begin{array}{l}F {H}_{1}=G {H}_{2}\\ {H}_{1}=\dfrac{\left|\left({C}_{y}-{A}_{y}\right){B}_{x}+\left({A}_{x}-{C}_{x}\right){B}_{y}+{A}_{y}{C}_{x}-{A}_{x}{C}_{y}\right|}{\sqrt{{\left({C}_{y}-{A}_{y}\right)}^{2}+{\left({A}_{x}-{C}_{x}\right)}^{2}}}\\ {H}_{2}=l \mathrm{cos}\alpha \end{array}\right. \text{,} $$ (5) 式中, F为油缸所受负载,H1 为油缸作用力对旋转中心的力臂,mm;H2 为吊重对旋转中心的力臂,mm;G 为举升臂受到的负载,N;l 为举升臂长度,mm。由式(5)可得:
$$ \begin{split} F= & Gl\mathrm{cos}\alpha \times \\ & \dfrac{\sqrt{{\left[{L}_{2}-d \mathrm{sin}\left(\alpha -\beta \right)\right]}^{2}+{\left[{L}_{1}-d\mathrm{cos}\left(\alpha -\beta \right)\right]}^{2}}}{\left|{-d\mathrm{cos}\left(\alpha -\beta \right) L}_{2}+d \mathrm{sin}\left(\alpha -\beta \right) {L}_{1}\right|} \text{。} \end{split} $$ (6) 根据式(6)计算,举升机构进行装卸时的油缸理论最大推力(F推)=8 440 N,最大拉力 (F拉)=11 499 N。吊卸过程油缸负载随举升臂旋转角度的变化曲线如图3 所示。
1.3 摆臂式装卸结构尺寸优化
由于设计的装卸范围较大,使得油缸在装卸初始位置和最终位置负载很大,且装卸结构很容易进入负载快速变化区间,导致油缸负载急剧增大,因此,对摆臂式装卸结构尺寸进行优化。本文建立ADAMS虚拟样机,进行结构优化,参数化建模主要涉及关键铰点A、B、C、D 点(图4)。根据各部件之间的运动关系在模型上添加运动副约束,各构件的具体形状对设计的影响很小[14]。本文模型主要用到的运动副约束有转动副、平动副、固定副,在装卸底座与大地之间添加固定副,运动关节处添加转动副,推杆和油缸之间添加平动副。
1.3.1 优化目标和优化变量的选取
为降低油缸负载,以油缸驱动力 (最大推力和最大拉力,F)最小作为目标进行优化,具体见下式:
$$ \mathrm{m}\mathrm{i}\mathrm{n}{\left|F\right|}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\left\{\begin{array}{c}\min{F}_{\mathrm{m}\mathrm{a}\mathrm{x}}\\ \max{F}_{\mathrm{m}\mathrm{i}\mathrm{n}}\end{array}\right. 。 $$ (7) 为了减小摆臂式装卸结构在起始和结束位置处的油缸负载,并使油缸负载变化更为平稳,本文参照聂阳文等[14]方法对摆臂式装卸结构铰点位置尺寸进行敏感度测试,并选择对优化目标影响较大的设计变量作为被优化设计变量,油缸F的敏感度见表1。由表1可见,序号 1~6最大推力对设计点坐标变量 DV_AY、DV_CX、DV_CY初始值的敏感度较大,最大拉力对 DV_AY、DV_CY 的敏感度较大;序号 7~8结构尺寸设计变量 DV_BC、DV_CBD对目标函数的敏感度均很大。说明初始结构下的缸体铰点竖直位置、推杆铰点至旋转中心距离、推杆铰点与举升臂偏角对油缸最大拉力和最大推力载荷有很大影响,故选择 DV_AY、DV_BC、DV_CBD 作为摆臂式装卸结构优化的设计变量。
表 1 设计变量对驱动力(F)的敏感度Table 1. Sensitivity of design variables to driving force (F)序号
No.变量
Variable最大推力敏感度
Sensitivity of
the max. thrust最大拉力敏感度
Sensitivity of
the max. tension1 DV_AX 5.582 2.700 2 DV_AY 61.379 32.866 3 DV_CX −29.330 −14.862 4 DV_CY −295.160 −254.710 5 DV_DX 0 −12.062 6 DV_DY −25.644 15.763 7 DV_BC −80.462 23.032 8 DV_CBD 701.140 374.030 1.3.2 约束条件的确定
摆臂式装卸结构铰点优化涉及的约束条件包括边界约束、传动角约束、油缸长度约束和几何约束。边界约束是指优化时设计变量的取值范围,即:
$ 0\leqslant \mathrm{D}\mathrm{V}\_\mathrm{A}\mathrm{Y}\leqslant 150\;{\mathrm{mm}} $ 、$ 100\;{\mathrm{mm}}\leqslant \mathrm{D}\mathrm{V}\_\mathrm{B}\mathrm{C}\leqslant 200\;{\mathrm{mm}} $ 、$ 30^\circ \leqslant \mathrm{D}\mathrm{V}\_\mathrm{C}\mathrm{B}\mathrm{D}\leqslant 40^\circ $ ;传动角约束是指为满足机构的传动特性需要而对传动角进行的限制,以避免出现机构运行至或接近死点位置,油缸的传动角$ \mathrm{\angle }ACB $ 取值范围为 10 °~ 170 °;油缸长度约束是指油缸在工作过程中2个铰点之间的距离应满足液压缸行程要求,根据液压缸型号,油缸2个耳环之间的距离为 500~780 mm,行程为 280 mm;几何约束是指保证运动三角形或四边形在任何工况下均成立的设定约束,针对摆臂式结构的优化需要保证 ΔABC和ΔCBD 满足内角定理,即:$$ \left\{\begin{array}{c}\angle ABC+\angle BCA+\angle CAB=180\\ \angle BCD+\angle CBD+\angle BDC=180\end{array}\right. 。$$ (8) 1.3.3 优化结果
在 ADAMS “优化”模块添加相应的目标函数、设计变量和约束条件后求解,优化前后设计变量与目标函数值的结果如表2 所示。由表2可见,优化后的最大驱动力从优化前的 11 802 N降低至10 387 N,降低了 12.0%。
表 2 优化前后设计变量与目标函数值Table 2. Design variable and objective function value before and after optimization优化
OptimizationDV_BC DV_CBD DV_AY 目标函数值/N
Objective function value前 Before 140.000 35.000 100.000 11 802 后 After 145.350 37.073 101.310 10 387 图5 为优化前后油缸驱动力变化曲线。由图5可见,优化后最大负载的降低体现在所需油缸负向驱动力降低,即降低了装卸结构在极限装卸位置所需的最大拉力,降低了 12.0%;起始位置的正向驱动力从 8 917 N增大到了 10 338 N,增加了 15.9%;优化前后的负载变化趋势较为相似,虽然降低了工作过程中的最大负载,但仍存在负载变化较为突兀的问题。这种液压冲击现象广泛存在于各类机械设备中,尤其是工程机械、农业机械、航空航天等设备中,是造成机械振动、液压管路破裂以及水锤现象的主要成因[15]。
2. 绳索联动装卸结构设计与优化
2.1 绳索联动装卸结构设计与分析
传统摆臂式结构装卸作业结构简单,但是工作范围小,在临界工作位置油缸负载较大且存在负载突变现象。针对该问题,本文在摆臂式装卸结构的基础上,设计一种绳索与举升臂联动的装卸结构,利用吊绳滑轮结构与摆臂结构联动扩大装卸作业的工作范围,避免负载突变。图6 为该结构初始和极限位置示意图,其主要结构包括摆臂式举升结构、滑轮 R和定滑轮r,其中, R 、r 分别铰接在举升臂上、下2个铰点,吊绳一端固定在举升结构底座上,从底座出发,吊绳先逆时针缠绕滑轮 R,再顺时针缠绕定滑轮 r,吊绳另一端连接负载。随着举升结构的运动,吊绳在滑轮 R 和定滑轮 r 上缠绕的弧长随之变化;随着举升臂旋转运动,虽然2个滑轮的相对位置不变,但滑轮上的绳索长度产生了变化,吊绳末端相对举升臂末端产生一个位移,绳索虽然没有驱动源,但随着举升臂的旋转产生了“联动”。
将2个滑轮、举升臂视为一个刚体,当举升臂摆角增大 ∆α,则下部2个滑轮上任意点的角位移为 ∆α,因此有 ∆γ1=∆γ2=−∆α;滑轮 R 上的缠绕钢丝绳弧长变化为 ∆l1=−∆αR,定滑轮 r 上的缠绕钢丝绳弧长变化为∆l2=−∆αr。设自由端初始时绳长为 l ,自由端 E 相对举升臂末端 D 的竖直位移(∆h )为:
$$ \Delta h=-\left(\Delta {l}_{1}+\Delta {l}_{2}\right)=-\dfrac{{\text{π}} \left(\alpha -{\alpha }_{0}\right)}{180}\left(R+r\right) \text{。} $$ (9) 滑轮半径 R+r越大,钢丝绳联动结构对装卸竖直位移的增益越明显,反之增益越小;考虑到竖直位移增益的影响,吊卸下降过程中可能导致货箱与运输机碰撞,为兼顾钢丝绳联动结构的增益效果,取R=50 mm、r=30 mm。具有吊绳联动结构的情况下,当举升臂旋转角度为 183.70°时,货箱可达到装卸极限位置,此时吊绳末端E相对举升臂最高点的竖直位移为 180.08 mm,位移增益效果明显。2种装卸结构货箱底部中心点轨迹见图7,摆臂式结构中的轨迹呈正圆弧形,而绳索联动结构因存在位移增益呈近似椭圆弧形。
装卸初始位置油缸受压表现为推力,将油缸视为二力杆,视举升臂、滑轮、钢丝绳为一个整体进行受力分析(图8)。设旋转中心 B 铰支水平方向受力为 Fx、竖直方向受力为Fy,以 B 为参考点,钢丝绳自由端对货物拉力(G) 、固定端底座对钢丝绳拉力(G′)、油缸驱动力(F)三力的力矩平衡为:
$$ {F H}_{1}+G' R=G \left({H}_{2}-r\right) $$ (10) 由式(5)和(10)可得,油缸驱动力(F)表达式:
$$ F=\dfrac{G \left(l \mathrm{cos}\alpha -R-r\right)\left|{-{L}_{3} \mathrm{cos}\left(\alpha -\beta \right) L}_{2}+{L}_{3} \mathrm{sin}\left(\alpha -\beta \right) {L}_{1}\right|}{\sqrt{{\left[{L}_{2}-{L}_{3} \mathrm{sin}\left(\alpha -\beta \right)\right]}^{2}+{\left[{L}_{1}-{L}_{3} \mathrm{cos}\left(\alpha -\beta \right)\right]}^{2}}}。 $$ (11) 油缸驱动力变化曲线如图9 所示,最大推力为 12 357 N,最大拉力为 7 983 N。由于举升臂更早到达极限装卸位置,在 183.70°时,提前到达了装卸位置,此时最大拉力比摆臂式装卸结构明显减小。
2.2 绳索联动装卸结构尺寸优化
在相同的摆臂结构下,绳索联动装卸结构可以使得举升臂提前到达极限装卸位置,进而避免油缸受到较大的拉力;受绳索滑轮结构的影响,在装卸起始阶段,驱动油缸承受较大负载且负载存在突变的现象。因此,既要保证油缸在工作中的负载不能太大,又要避免负载突变。其尺寸优化属于多目标优化问题,优化模型通常可描述为:
$$ \left\{\begin{array}{l} {\mathrm{min}}F\left(x\right)={\left[{f}_{1}\left(x\right),{f}_{2}\left(x\right),\cdots ,{f}_{n}\left(x\right)\right]}^{{\mathrm{T}}}\\ {\mathrm{s.t.}}\;{{x}}\in \varOmega \\ \varOmega =\left\{x\in {R}^{n}|{g}_{i}\left(x\right)\leqslant 0,i=\mathrm{1,2},\cdots ,p\right\}\end{array}\right. \text{,} $$ (12) 式中,F(x) 为优化模型的目标空间,f1(x), f2(x), …, fn (x) 为优化模型的目标函数,
$ {g}_{i} $ (x) 为模型中的各种约束条件,如线性约束、非线性约束、边界约束等,$ \varOmega $ 为x=(x1, x2, …, xn) 所在的空间(决策空间)。遗传算法在复杂工程问题求解中应用广泛[16-20]。采用遗传算法对目标进行优化求解,为解决目标间的冲突导致多目标优化可能并不存在最优解的问题,本文利用基于精英策略的快速非支配排序遗传算法(Non-dominated sorting genetic algorithms Ⅱ,NSGA-Ⅱ)求 Pareto 最优解,算法流程见图10。绳索联动装卸结构油缸负载受到举升臂工作状态、结构尺寸等因素的影响,优化前各尺寸参数为:油缸铰点到举升臂旋转中心水平距离(L1)为 640 mm、竖直距离(L2)为101.43 mm,举升臂铰点到旋转中心距离(L3)为145.35 mm,举升臂长度(l)为 600 mm,举升臂铰点偏角(β)为 37.07°,举升臂起始角(α0)为 52.93°,举升臂极限角(α1)为 183.70°,滑轮半径(R)为 50 mm,滑轮半径(r)为 30 mm。
2.2.1 目标函数的确定
由受力分析可知,举升臂工作状态、油缸铰点位置、推杆铰点位置、滑轮尺寸等都会对油缸负载产生影响。以起始位置推力 f1(x)、起始位置推力变化率 f2(x) 和最终位置拉力 f3(x) 作为优化目标:
$$ \left\{\begin{array}{l}{f}_{1}\left(x\right)=F\left({L}_{1},{L}_{2},{L}_{3},\beta ,\alpha \right){|}_{\alpha ={\alpha }_{0}}\\ {f}_{2}\left(x\right)=-\dfrac{dF\left({L}_{1},{L}_{2},{L}_{3},\beta ,\alpha \right)}{d\alpha }{|}_{\alpha ={\alpha }_{0}}\\ {f}_{3}\left(x\right)=-F\left({L}_{1},{L}_{2},{L}_{3},\beta ,\alpha \right){|}_{\alpha ={\alpha }_{1}}\end{array}\right. 。 $$ (13) 2.2.2 优化设计变量的选择
选取L1、L2、L3、β和α1作为设计变量(x),x计算如下:
$$ x={\left[{L}_{1},{L}_{2},{L}_{3},\beta ,{\alpha }_{1}\right]}^{{\mathrm{T}}}。 $$ (14) 2.2.3 边界和约束设置
综合考虑装卸结构在单轨运输机上的布置和安装,设计变量边界条件[单位:mm,(º)]设置如下:
$$ \left\{\begin{array}{l}{L}_{1}\in \left(\mathrm{600,650}\right)\\ {L}_{2}\in \left(\mathrm{0,150}\right)\\ {L}_{3}\in \left(\mathrm{100,200}\right)\\ \beta \in \left(\mathrm{30,40}\right)\\ {\alpha }_{1}\in \left(\mathrm{170,190}\right)\end{array}\right. 。 $$ (15) 举升臂角度 α 和滑轮半径 R 需满足非线性条件,并在最终角度 α1 时到达装卸极限高度位置,满足下式:
$$ \left\{\begin{array}{l}{P}_{y}\left(\alpha ,R\right)=l \left(\mathrm{sin}\alpha -\mathrm{sin}{\alpha }_{0}\right)-\dfrac{{\text{π}} \left(\alpha -{\alpha }_{0}\right)}{180}\left(R+r\right)\\ {P}_{y}\left({\alpha }_{1},R\right)=-700\end{array}\right. \text{。} $$ (16) 装卸过程中推杆长度(AC/mm)与设计变量满足以下关系,并且推杆长度应在设计的范围内:
$$ \left\{ \begin{array}{l}AC\left({{L}_{1},{L}_{2},L}_{3}\right)=\\ \quad \sqrt{{\left({L}_{2}-{L}_{3}\cdot \mathrm{sin}\left(\alpha -\beta \right)\right)}^{2}+{\left({L}_{1}-{L}_{3}\cdot \mathrm{cos}\left(\alpha -\beta \right)\right)}^{2}}\\ 500\leqslant AC\left({{L}_{1},{L}_{2},L}_{3}\right)\leqslant 780\end{array}\right. 。 $$ (17) 2.2.4 优化过程及结果
在 MATLAB 软件中编程,采用 NSGA-Ⅱ 算法进行多目标优化求解,并对目标函数进行求解设置。设定初始样本数量为 100 ,每次迭代样本数为 100 ,为了保证多目标遗传算法的收敛性与精确性,设置最大允许帕累托百分比为 70%、最大迭代次数为 100,得到函数前 70 个 Pareto 解集及目标函数值,如图11 。
基于模糊优选理论[21],在多目标优化计算所得相对最优解基础上开展模糊评价分析。样本数据的结构尺寸、举升臂工作最大角度均满足装卸工作时油缸长度和角度,以油缸最大推力、起始推力变化率、油缸最大拉力这 3 个目标函数作为评价指标开展模糊综合评价。由于这 3 个目标函数中存在数量级差别,需要进行评价指标的归一化处理,建立不同评价指标偏好的权重系数,根据综合评价得分(K)得到不同评价标准下的优化方案:
$$ \left\{\begin{array}{l} K={\boldsymbol{\omega}} {\boldsymbol{M}}={\omega }_{1}{M}_{1}+{\omega }_{2}{M}_{2}+{\omega }_{3}{M}_{3}\\ {\boldsymbol{\omega}} \in \left[\mathrm{0.4,0.2,0.4}\right]\end{array}\right. \text{,} $$ (18) 式中,
$ {\boldsymbol{\omega}} $ 为权重矩阵,$ {\omega }_{1} $ 、$ {\omega }_{2} $ 、$ {\omega }_{3} $ 分别为油缸最大推力、起始推力变化率、油缸最大拉力的权重系数;$ {\boldsymbol{M}} $ 为归一化后的评价指标矩阵,$ {M}_{1} $ 、$ {M}_{2} $ 、$ {M}_{3} $ 分别为油缸最大推力、起始推力变化率、油缸最大拉力对应指标,计算公式为:$$ {M}_{i}=\dfrac{{f}_{i}-{f}_{{\mathrm{min}}}}{{f}_{{\mathrm{max}}}-{f}_{{\mathrm{min}}}},i\in \left(\mathrm{1,2},3\right)。 $$ (19) 驱动力变化曲线如图12。最终得到优化后的绳索联动装卸结构,最大推力(F推)=5 697 N,最大拉力 (F拉)=9 203 N。摆臂式装卸结构优化前后和绳索联动装卸结构优化前后对应的目标函数如表3 所示,通过遗传算法优化后的最大驱动推力相比传统的摆臂式装卸结构降低了 41.2%、最大驱动拉力降低 10.3%,最大驱动推力变化率降低 53.0%,说明在绳索联动结构下油缸负载更小、变化更加平稳。
表 3 优化前后参数与优化目标值对比Table 3. 3 Comparison of parameters and objective object values before and after optimization结构1)
Structure优化
OptimizationL1/mm L2/mm L3/mm β/(°) α1/(°) R/(°) r/(°) f1/N f2/[N·(°)−1] f3/N Ⅰ 前 Before 640 100.00 140.00 35.00 199.47 / / 8440 872 11499 后 After 640 101.31 145.35 37.07 199.47 / / 9694 1168 10263 Ⅱ 前 Before 640 101.31 145.35 37.07 183.70 50 30 12357 2149 7983 后 After 642 40.00 150.00 35.00 183.12 53 30 5697 549 9203 1) Ⅰ:摆臂式结构,Ⅱ:绳索联动结构。
1) Ⅰ: Swing arm structure, Ⅱ: Rope linkage structure.3. 绳索联动装卸结构动力学仿真
3.1 绳索联动装卸结构虚拟样机建模
ADAMS虚拟样机技术可以很好地模拟机构动态性能,在机械设计中被广泛应用[22-23]。本文建立了单轨运输机自装卸装置ADAMS虚拟样机,以研究前文中设计的绳索联动装卸结构的可行性。
对于绳索联动装卸结构来说,货箱与举升臂并非刚性连接,而是采用柔性的绳索连接。要建立的绳索联动装卸装置虚拟样机系统属于刚柔耦合多体系统。利用有限元建立钢丝绳柔性体过于复杂,由于钢丝绳的螺旋结构以及钢丝之间复杂的接触关系,构建的钢丝绳有限元模型需要划分大量的网格[24]。虚拟样机中的绳索包括缠绕滑轮的绳索和连接货箱与锁具的绳索,绳索联动装卸的仿真重点在于模拟绳索的弯曲、缠绕等的传动效果。绳索建模如图13 所示,对于缠绕滑轮的绳索,绳索与滑轮之间存在大量的接触交互,采用Machinery cable模块离散法模拟绳索与滑轮的缠绕运动;对于连接货箱与锁具的绳索,绳索只起到连接和传力的作用,参考陈松阳等[25]的方法将整条绳索分割成多个小段,每个小段可以视为单个刚体,在2个相邻的刚体之间添加轴套力,完成钢丝绳柔性体的近似模拟;为了模拟绳索联动装卸结构的负载情况,还要在模型中建立重物、地面模型,设置接触,尽可能模拟真实环境。
3.2 动力学仿真结果
装卸过程货箱左右两端及举升臂上部铰点的运动轨迹如图14,运动轨迹符合预期。
液压油缸驱动力、举升臂旋转角度、油缸角度随时间的变化曲线如图15。装卸过程举升臂旋转角度变化值为 130.95°,液压油缸角度绝对变化值为 2.08°、最大变化值为 9.21°。在吊卸起始瞬间,驱动力陡增并稳定在6 264 N后逐渐下降;在 26.2 s时,驱动力达到极值为−9 489 N后迅速减小;在27.1 s时完全落地,驱动力为−345 N。在 30 s时,绳索被拉紧,油缸驱动力大小陡增并迅速稳定到−9 222 N开始吊装,吊装过程驱动力变化趋势与吊卸过程相反。仿真的结果与理论分析一致,说明尺寸设计符合要求。
4. 测试结果与分析
完成装卸装置相关零部件的加工、组装和调试后,在华南农业大学工程学院的单轨运输机试验场安装,并进行载质量装卸测试(图16)。分别进行总质量为 0~200 kg砝码载质量测试,测量进行吊卸和吊装的时间,重复 5 次,对装卸装置在不同总载质量装卸时间的采集结果求平均值,结果见表4。装卸装置在 0~200 kg装卸载质量下的吊卸时间为 16.7~18.7 s、吊装时间为 19.1~19.9 s。
表 4 不同总装载质量的装卸时间Table 4. The loading or unloading time with different total masst/s 项目 Item 0 kg 50 kg 100 kg 150 kg 200 kg 吊卸 Unloading 18.69 18.54 18.00 16.94 16.69 吊装 Loading 19.94 19.59 19.42 19.15 19.07 吊卸和吊装时,驱动力都经历了从正负载方向到负负载方向的转变。在正负载方向,液压系统需要克服负载的阻力,因此,油缸速度可能相对较慢;负负载方向与油缸活塞运动方向相同,即负载帮助油缸推动,油缸速度可能会加快。装卸过程中的摆动测试结果(图17)显示,货箱满载时吊卸和吊装水平方向加速度范围分别为−1.00~1.10和−0.75~0.90 m/s−2,空载时分别为−0.60~0.55和−0.40~0.30 m/s−2;货箱摆动均呈现开始时幅值较大,随装卸过程摆动变小并趋于0的特点,这是因为举升臂启动瞬间的加速度使货箱产生一定的摆动,但随着举升臂装卸过程中运动较为平稳,摆动幅度逐渐衰减。货箱除了受到举升臂运动的影响外,还受到绳索的振动和张紧力等影响。总之,装卸装置在满载和空载情况下进行装卸的过程中,货箱摆动幅度较小,运动比较平稳。
5. 结论
本文针对山地果茶园的物资装卸问题,设计了单轨运输机摆臂式装卸方案,对传统的摆臂式装卸结构进行了分析,通过参数化设计与敏感度分析,得到油缸负载敏感尺寸,并对其进行优化,使摆臂式装卸结构最大负载降低了12.0%。针对传统摆臂式装卸结构存在负载大、负载突变的问题,设计了一种绳索联动装卸结构,分析位移增益原理和受力情况,并利用 NSGA-Ⅱ 算法优化结构尺寸,优化后的理论最大驱动推力为5 697 N、最大驱动拉力为9 203 N,相比传统的摆臂式装卸结构,理论最大驱动推力降低了41.2%、最大驱动拉力降低 10.3%、最大驱动推力变化率降低 53.0%,显著提升了摆臂装卸性能。绳索联动装卸的动力学仿真验证了理论分析的正确性。对试制的样机进行了载质量测试和摆动测试,表明该结构可行。相比传统摆臂式装卸结构,本文提出的具有绳索联动结构的摆臂式装卸结构具有更好的性能,可以在运输装卸领域推广应用。
-
表 1 各处理营养液中氮磷钾浓度1)
Table 1 N, P and K contents in nutrient solution of each treatment

-
[1] 冯宏, 郭彦彪, 韦翔华, 等.赤红壤丘陵坡地不同侵蚀部位土壤养分和微生物特征变异性研究[J].水土保持学报, 2008, 22(6):149-152. doi: 10.3321/j.issn:1009-2242.2008.06.032 [2] 郑本暖, 叶功富, 卢昌义.干旱胁迫对4种植物蒸腾特性的影响[J].亚热带植物科学, 2007, 36(1):36-38. doi: 10.3969/j.issn.1009-7791.2007.01.010 [3] 潘伟彬, 邓恢.4种草本水土保持植物的耐旱生理特性[J].华侨大学学报:自然科学版, 2009, 30(3):305-308. http://d.old.wanfangdata.com.cn/Periodical/hqdxxb200903016 [4] 戴文娇, 宁平, 刘晓海, 等.类芦对铅的耐性及富集能力探讨[J].环境工程学报, 2008, 2(7):1004-1008. http://d.old.wanfangdata.com.cn/Periodical/hjwrzljsysb200807029 [5] 冯宏, 戴军, 李永涛, 等.重金属和pH值对类芦种子萌发的影响[J].水土保持通报, 2010, 30(6):96-99. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201002922219 [6] 王炜, 孙发政, 刘荣堂.类芦对重建边坡防护植被的贡献[J].草原与草坪, 2006(4):49-51. doi: 10.3969/j.issn.1009-5500.2006.04.011 [7] 袁剑刚, 周先叶, 陈彦, 等.采石场悬崖生态系统自然演替初期土壤和植被特征[J].生态学报, 2005, 25(6):1517-1522. doi: 10.3321/j.issn:1000-0933.2005.06.042 [8] 林武星, 陈东华, 倪志荣, 等.闽南沿海石矿区植物配置模式对水土保持的影响[J].防护林科技, 2006(4):1-3. doi: 10.3969/j.issn.1005-5215.2006.04.001 [9] 陆海波, 刘方, 朱健, 等.煤矿石堆场自然植被优势植物根际有效态重金属含量[J].生态学杂志, 2012, 31(12):3207-3212. [10] 秦建桥, 夏北成, 胡萌, 等.广东大宝山矿区尾矿库植被演替分析[J].农业环境科学学报, 2009, 28(10):2085-2091. doi: 10.3321/j.issn:1672-2043.2009.10.015 [11] 刘惠娜, 杨期和, 杨和生, 等.粤东铅锌尾矿三种优势植物对重金属的吸收和富集特性研究[J].广西植物, 2012, 32(6):743-749. doi: 10.3969/j.issn.1000-3142.2012.06.005 [12] 郭彦彪, 冯宏, 周波, 等.广东大宝山矿区废石场土壤酸化特征分析[J].水土保持学报, 2013, 27(6):46-50. doi: 10.3969/j.issn.1009-2242.2013.06.010 [13] 唐启义. DPS数据处理系统:实验设计、统计分析及数据挖掘[M].北京:科学出版社, 2010: 74-97. [14] 郭孝, 陈二秋.中原地区多年生禾草物候期特点与分蘖动态的研究[J].草业科学, 2002, 19(6):35-38. doi: 10.3969/j.issn.1001-0629.2002.06.011 [15] 殷国梅, 刘德福.沙生冰草分蘖特性的初探[J].中国草地, 2004, 26(3):75-77. http://d.old.wanfangdata.com.cn/Periodical/zgcd200403015 [16] 林夏馨.类芦生长和抗逆特性的分析探讨[J].亚热带水土保持, 2006, 18(1):48-51. doi: 10.3969/j.issn.1002-2651.2006.01.015 [17] 蔡丽平, 吴鹏飞, 侯晓龙, 等.类芦根系对不同强度干旱胁迫的形态学响应[J].中国农学通报, 2012, 28(28):44-48. doi: 10.3969/j.issn.1000-6850.2012.28.008 [18] 米国华, 邢建平, 陈范骏, 等.玉米苗期根系生长与耐低磷的关系[J].植物营养与肥料学报, 2004, 10(5):468-472. doi: 10.3321/j.issn:1008-505X.2004.05.004 [19] 李海波, 夏铭, 吴平.低磷胁迫对水稻苗期侧根生长及养分吸收的影响[J].植物学报, 2001, 43(11):1154-1160. doi: 10.3321/j.issn:1672-9072.2001.11.010 [20] 万延慧, 年海, 严小龙.大豆种质耐低磷与耐铝毒部分指标及其相互关系的研究[J].植物营养与肥料学报, 2001, 7(2):199-204. doi: 10.3321/j.issn:1008-505X.2001.02.014 [21] 蔡丽平, 吴鹏飞, 侯晓龙, 等.磷胁迫对水土保持先锋植物类芦光合特性的影响[J].水土保持学报, 2012, 26(6):281-285. http://d.old.wanfangdata.com.cn/Periodical/trqsystbcxb201206055 [22] 安琼, 王丽敏, 张鹏, 等.不同钾浓度对玉米幼苗生长的影响[J].中国农学通报, 2011, 27(5):115-119. http://d.old.wanfangdata.com.cn/Periodical/zgnxtb201105023 [23] 孙发政.类芦的固土护坡性状及其生产应用价值[J].草原与草坪, 2004(1):66-69. doi: 10.3969/j.issn.1009-5500.2004.01.020 [24] CONESA H M, ROBINSON B H, SCHULIN R, et al. Growth of Lygeum spartum in acid mine tailings: Response of plants developed from seedlings, rhizomes and at field conditions[J]. Environ Pollut, 2007, 145(3):700-707. doi: 10.1016/j.envpol.2006.06.002
[25] 闫良, 茶正早, 罗微, 等.3种母质砖红壤中钾素垂直运移特征初步研究[J].热带作物学报, 2012, 33(10):1749-1757. doi: 10.3969/j.issn.1000-2561.2012.10.007 [26] 闫良, 茶正早, 罗微, 等.5种不同母质土壤上硝态氮垂直运移特征初步探讨[J].热带农业科学, 2011, 31(3):24-29. doi: 10.3969/j.issn.1009-2196.2011.03.006 [27] MATULA J. Relationship between phosphorus concentration in soil solution and phosphorus in shoots of barley[J]. Plant Soil Environ, 2011, 57(7):307-314. doi: 10.17221/PSE
[28] 杨建军, 冉炜, 沈其荣.小麦生长季节太湖地区土壤溶液中氮磷浓度的变化[J].南京农业大学学报, 2002, 25(2):66-70. http://d.old.wanfangdata.com.cn/Periodical/njnydxxb200202015 [29] 张志权, 束文圣, 廖文波, 等.豆科植物与矿业废弃地植被恢复[J].生态学杂志, 2002, 21(2):47-52. doi: 10.3321/j.issn:1000-4890.2002.02.012




 下载:
下载: